• Strona główna
• Blog
• Statystyka w analityce internetowej – jakie korzyści dają testy porównawcze?

Statystyka w analityce internetowej – jakie korzyści dają testy porównawcze?

Porównywanie dwóch lub więcej średnich wartości to jedna z najczęstszych analiz wykonywanych przy pracy z danymi. Na przystępnym przykładzie dowiesz się, w jaki sposób wykorzystać statystykę, by upewnić się, że przewaga jednej marki nad drugą nie jest kwestią przypadku. Znajdziesz też kilka linków, dzięki którym możesz poszerzyć swoją wiedzę.

 

Porównywanie dwóch średnich

Może zadajesz sobie pytanie: „Po co mówić o testach statystycznych w przypadku porównywania dwóch średnich?”. Robisz to zapewne bardzo często. Gołym okiem widać, która średnia jest większa, a która mniejsza.
Użyjmy jednak następującego przykładu. Wyobraź sobie, że sprzedajesz sportowe buty. Dwie marki (A i B) przynoszą ci wyjątkowo dobry przychód i planujesz poszerzyć ich asortyment. Nie wiesz jednak, czy korzystniej będzie zainwestować w oba produkty po równo, czy może w jeden z nich nieco bardziej – a jeśli tak, to w który?

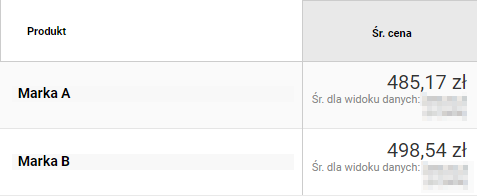
Google Analytics: Porównanie średniej ceny dla produktów dwóch kategorii z wykorzystaniem segmentacji.

W Google Analytics sprawdzasz, jak wyglądała sprzedaż obu marek dla ostatniego miesiąca. Marka B przyniosła średnio o 2,8%więcej przychodów – na każdy zakup. Może się to wydawać niewielką różnicą, ale przy utrzymywaniu się przez dłuższy czas takich wyników, oznacza to ponad 13 tys. zł przychodu więcej – na każde tysiąc zamówień.
Zatem marka B wydaje się bardziej atrakcyjną opcją. Pytanie jednak brzmi: „Na ile różnica między tymi średnimi jest istotna? Jaką możesz mieć pewność, że to nie kwestia przypadku?”. W tym celu pod uwagę musimy wziąć średnie ceny dla poszczególnych produktów z danej marki.
Na potrzeby tego artykułu wygenerowaliśmy po 40 takich cen. Na poniższych histogramach zobaczyć można, że za jednoznacznie różniącymi się średnimi cenami marek stoją już nie tak jednoznacznie różne rozkłady średnich cen produktów.

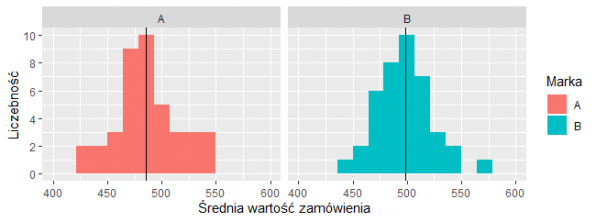
Rozkład średnich cen produktów marki A i B wraz ze średnią dla marki (linia pionowa).

W tej sytuacji wykorzystać możemy test t-Studenta (o którego piwnej genezie wspominaliśmy w artykule o 5 krokach statystycznej analizy danych w Google Analytics). Wymaga on jednak spełnienia kilku założeń, o których przeczytać możesz na przykład tutaj. W przypadku ich nie spełnienia wykonać należy odpowiedni test nieparametryczny – w tym przypadku test U Manna-Whitney’a.
Test t pozwala na porównywanie średnich dla dwóch grup (niezależnych, tj. takich, których elementy są względem siebie niezależne) i obliczenie istotności statystycznej różnicy między nimi, z uwzględnieniem każdej pojedynczej obserwacji (w naszym przypadku: wyników poszczególnych produktów). Pozwala to na znacznie głębsze i pewniejsze porównanie wyników dwóch interesujących cię grup niż proste zestawienie ze sobą ich średnich wyników.
Wynikiem testu jest wartość p, która w dużym uproszczeniu informuje o tym, czy porównywane grupy istotnie się od siebie różnią. Wniosek o istotności tej różnicy możemy wyciągnąć, gdy wartość p będzie mniejsza niż 0,05, czyli powszechnie przyjmowany poziom istotności. W omawianym przypadku wartość p w teście t-Studenta wyniosła 0,046. Niewiele poniżej progu, ale wystarczająco by dać nam statystyczną pewność przewagi marki B nad marką A.

 

Inne metody porównywania średnich

Porównywać średnie możemy także np. przy porównywania różnych wariantów kolorowych produktów. W takim przypadku skorzystać możesz z testu t dla prób zależnych, to jest takich, których poszczególne obserwacje (tutaj: produkty) można połączyć w jednoznaczne pary (np. dwa produkty różniące się wyłącznie wersją kolorystyczną). Podobnie jak w przypadku testu dla prób niezależnych, gdy nie spełnia założeń testu t, należy skorzystać z wersji nieparametrycznej: Testu Wilcoxon’a.
Często jednak możesz chcieć porównać więcej niż tylko dwie grupy produktów, użytkowników itp. W takim przypadku również masz do dyspozycji odpowiedni test – analizę wariancji (ANOVA). Można ją wykorzystać zarówno w próbach niezależnych jak i zależnych.
Więcej o teście t, a także jego nieparametrycznych odpowiednikach, które należy stosować przy niespełnieniu jego założeń znajdziesz m.in. tutaj. Z kolei kalkulatory pozwalające obliczyć wynik testu znajdziesz np. na Social Science Statistics lub w Excel’u. Wystarczy podać wartości porównywanych grup, a kalkulator obliczy dla nas wartość p!
Poniżej znaleźć można średnie ceny, które zostały wykorzystane w powyższym przykładzie. Jeśli temat cię zainteresował i przeczytałeś już, jakie założenia muszą spełnić dane, zachęcamy do eksperymentowania z nimi! Drobna podpowiedź: jednym z testów na normalność rozkładu jest test Kołmogorowa-Smirnowa.

Ponieważ we właściwych analizach bierze się pod uwagę często znaczną liczbę zmiennych i wykonuje różnorodne testy i inne operacje na danych, w omawianych przykładach wykorzystano konieczne uproszczenia.
W Semahead bardzo dobrze rozumiemy potrzebę realizowania testów porównawczych i z chęcią Ci w tym pomożemy. Zgłoś się do nas! 

Zapisz się do newslettera i otrzymaj bezpłatnie e-book!

Zapisz mnie

Semahead

415 wpisów

Zobacz wszystkie wpisy